黄 铃1 李赢世1 王跃军1 阙志武2
(1.湖南省长沙市麓山梅溪湖实验中学 2.江西省南城一中)
在一些问题中,我们无法或者没有必要进行精确计算和判断,只需得出大概数值或数量级即可,这时就要用到估算法.估算法在生活及物理学习中具有重要作用.我们在处理某些物理问题时,可通过大致的合理的推算,忽略次要因素,考虑主要因素,通过选择有效信息,可以排除一些干扰因素,对问题进行合理近似.估算法在高中物理中应用广泛,在教材及高考试题中频繁出现.下面我们从5个方面总结估算法的应用.
1 运用生活常识解决估算问题
例1 某高中生从教学楼的一楼走上五楼,请估算在此过程中该学生克服重力做功最接近于( ).
A.7×102J B.7×103J
C.7×104J D.7×105J
解析 假设该高中生质量为60kg,重力加速度g取10m·s-2,每层楼高约3 m,一楼到五楼高度差约为12m,计算得W=mgh=7.2×103J,故而估算出选项B最为接近.
点评 解决该类题目,我们需要观察生活,熟记生活中的常见数值,譬如一个鸡蛋的质量为50~60g,中学生的质量为50~80kg,人走路的速度是1.1~1.5m·s-1,普通人骑自行车的速度是2.8~5.6m·s-1,一般楼层每层的高度是3m,国内火车铁轨标准轨距是1435mm,成年人一步的距离是45~65cm等.
例2 2023年10月4日,在杭州亚运会田径项目男子跳高决赛中,身高为1.92m 的卡塔尔选手穆塔兹·巴尔沙姆以破赛会纪录的2.35m 成绩夺冠.据此可估算出他起跳时竖直向上的速度约为( ).
A.2m·s-1 B.4m·s-1
C.5m·s-1 D.7m·s-1

图1
解析 起跳前该运动员的重心高度约为

×1.92m=0.96m,则由题可知,起跳过程中,该运动员的重心上升的最大高度为H =2.35 m-0.96 m=1.39m,根据竖直上抛运动规律可得,该运动员起跳时竖直向上的速度约为

≈5m·s-1,故选C.
点评 本题先将运动员的重心高度近似为身高的一半,再对最后的速度进行估算,进而得到正确选项.本题以杭州亚运会跳高为情境,将体育竞技和物理知识相结合,引导学生关注体育赛事,积极进行体育锻炼.
2 运用物理、数学常数解决估算问题
例3 (2023年全国乙卷)2022年10月,全球众多天文设施观测到迄今最亮伽马射线暴,其中我国的“慧眼”卫星、“极目”空间望远镜等装置在该事件观测中作出重要贡献.由观测结果推断,该伽马射线暴在1分钟内释放的能量量级为1048J.假设释放的能量来自于物质质量的减少,则每秒钟平均减少的质量量级为(光速为3×108 m·s-1)( ).
A.1019kg B.1024kg
C.1029kg D.1034kg
解析 根据质量亏损公式ΔE=Δmc2,代入题目所给数据,由上式可得每秒钟平均减少的质量约为1.9×1029kg,即每秒钟平均减少的质量量级为1029,所以选项C正确.
点评 本题涉及必备知识为质量亏损公式,用到了基本常数光速,主要考查考生的理解能力及物理学科核心素养中的物理观念,突出考查学生的估算能力.题目以科学研究中最新的重大科学事件为背景设计问题,彰显我国在国际社会上的科技成就和贡献,提升学生的民族自豪感,同时激励学生了解科学前沿,激发学生探索宇宙的兴趣.
例4 假设“天宫二号”正以速度v=7.8km·s-1绕地球做匀速圆周运动,试估算“天宫二号”距离地球表面的高度h.
解析 设“天宫二号”的轨道半径为r,质量为m,地球质量为M,地球半径为R,地球表面重力加速度为g,由公式
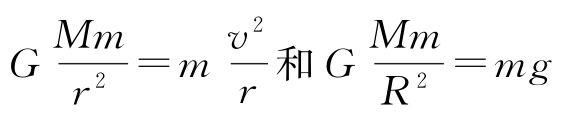
,得
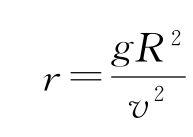
,代入数据得r≈6730km,故而“天宫二号”距离地球表面的高度h≈330km.
点评 本题给出的具体数值只有一个,但是我们通过万有引力的两个公式,发现要想估算出结果,只需要知道地球表面重力加速度和地球的半径即可.解答该类估算题时,我们应尽量熟记相关的物理及数学常数,譬如π2≈10,月球表面重力加速度约为地球表面重力加速度的六分之一,当角度很小时sinθ≈tanθ≈θ,光速c=3×108 m·s-1,地球表面加速度g 取10 m·s-2,万有引力常数、普朗克常数、空气中声速、电子的电荷量、分子直径、可见光波长和频率等的数量级,地球同步卫星的轨道半径,近地卫星的周期、线速度,地球的质量、半径,月亮的质量,太阳的质量等.
3 运用数学知识解决估算问题
人教版必修一教材对于匀变速直线运动位移公式的推导,运用数学微分法将运动分成很多小段,每一小段起始时刻物体的瞬时速度作为该段的平均速度,将各小矩形的面积之和近似代表物体在整个过程中的位移大小.推导过程所使用的微元法及近似法有助于培养学生的科学思维,提升学生解决问题的能力,便于之后的物理学习.
例5 有一架照相机,其光圈(进光孔径)随被摄物体的亮度自动调节,而快门(曝光时间)是固定不变的.为估测这架照相机的曝光时间,实验者从某砖墙前的高处使一个石子自由落下,拍摄石子在空中的照片如图2所示.由于石子的运动,它在照片上留下了一条模糊的径迹.已知石子从地面以上2.5m 的高度下落,每块砖的平均厚度为6cm,请估算这张照片的曝光时间.

图2
解析 该题体现了估算的特征,由图片可知,径迹表示的长度约为Δx=0.12m,径迹初始点到地面的高度约为0.51m.从石子初始位置下落至径迹初始点的位移约为

石子做自由落体运动,根据

,代入数据得石子在径迹初始点的速度约为v=6.25m·s-1.由于曝光时间极短,石子近似做匀速直线运动,故曝光时间为

点评 我们在物理教与学中要充分利用教材、挖掘教材,使我们的教学回归课标、回归教材.人教版物理新教材里面的“拓展学习”及课后“练习与应用”出现大量贴近生活情境的问题,旨在引导学生学会用物理思维和方法去观察生活,在生活中灵活运用物理及数学知识,应用更多的科学方法去解决问题.
例6 (2016年全国新课标Ⅰ卷)利用三颗位置适当的地球同步卫星,可使地球赤道上任意两点之间保持无线电通讯.目前,地球同步卫星的轨道半径约为地球半径的6.6倍.假设地球的自转周期变小,若仍仅用三颗同步卫星来实现上述目的,则地球自转周期的最小值约为( ).
A.1h B.4h
C.8h D.16h
解析 若地球自转周期变小,由公式

得

,知此时同步卫星的轨道半径也应随之变小,要实现三颗卫星覆盖全球的目的,由数学几何关系可作出图3.

图3
设地球半径为R,地球同步卫星的轨道半径为r1,周期为T1,满足题意后卫星的轨道半径为r2,周期为T2,由几何关系得之后卫星的轨道半径r2 =2R,由开普勒第三定律

,代入题中数据,得

本题还可以通过估算

进行求解,由开普勒第三定律得
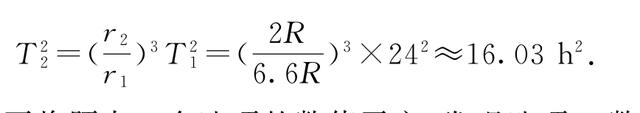
再将题中4个选项的数值平方,发现选项B数值平方后最接近,故而选项B符合题意.
点评 天体问题中数学的近似规律方法应用广泛.数学是学习物理的重要工具,渗透于物理学习的全过程,我们在平时的教与学中要注重培养学生运用数学方法和技巧解决问题的能力.
4 运用图像解决估算问题
对于物理中的图像问题,我们需从图像纵、横坐标的物理意义和图像中“点”“线”“斜率”“截距”和“面积”等诸多方面寻找解题的突破口.高考及教材中常通过图像估算解决一些问题.
例7 (2022年河北卷)科学训练可以提升运动成绩,某短跑运动员科学训练前后百米全程测试中,速度v 与时间t的关系图像如图4所示.由图像可知( ).

图4
A.0~t1 时间内,训练后运动员的平均加速度大
B.0~t2 时间内,训练前、后运动员跑过的距离相等
C.t2~t3 时间内,训练后运动员的平均速度小
D.t3 时刻后,运动员训练前做减速运动,训练后做加速运动
解析 根据v-t图像的斜率表示加速度,由题图可知0~t1 时间内,训练后运动员的后段图像的平均加速度比训练前的小,故选项A 错误;根据v-t图像围成图形的面积表示位移,由题图可知0~t2 时间内,训练前运动员后段时间跑过的距离比训练后的大,故选项B错误;由题图可知t2~t3 时间内,训练后运动员的位移比训练前的位移大,可知训练后运动员的平均速度大,故选项C错误;t3 时刻后,运动员训练前做减速运动,运动员训练后做加速运动,故选项D正确.
点评 对于该类v-t图像问题我们一般通过对图像斜率、截距、交点及图像与坐标轴所围图形的面积进行分析,近似估测相关物理量之间的关系.在平时的图像教学中,我们应多引导学生学会从图像中获取有用信息,并能对信息进行加工和处理.
例8 在做用油膜法估测油酸分子的大小实验时,每103mL 油酸酒精溶液中有纯油酸1 mL.用注射器测得58 滴这样的溶液为1mL.把1滴这样的溶液滴入盛水的浅盘里,等油膜形状稳定后,把玻璃板盖在浅盘上并描画出油膜的轮廓,如图5所示.图中正方形小方格的边长为1cm.

图5
(1)1滴油酸酒精溶液中含有的纯油酸的体积是多少?
(2)油膜的面积是多少?
(3)按以上数据,估算油酸分子的大小.
解析 (1)设1滴油酸酒精溶液中所含纯油酸的体积为V,则

(2)由图5可知,油酸大约占257个小格,故油酸面积

(3)油酸分子的直径

点评 本题通过油膜法估算分子直径的大小,解答本题时我们假设油酸分子之间不发生重叠,且不存在分子间隙,如此即构成了一个单分子油膜,我们用1滴油酸溶液体积与最终形成的油膜面积作比,即可得到分子的直径,我们在选取油膜所占小格时,超过半格的算一个,小于半格的忽略,这显然是一种忽略次要因素考虑主要因素的理想化的建模操作.
5 结合量纲解决估算问题
例9 通电直导线的周围会存在磁场,但磁感应强度B会有多大,同学们并不清楚.已知通电直导线周围空间某点的磁感应强度B 的大小与直导线中电流I 的大小和该点到直导线的距离d 有关.下面给出B 的四个表达式中只有一个是合理的,你可以通过一定的物理分析,对下列表达式的合理性作出判断,其中μ0 为真空中磁导率,单位为韦伯·(安培·米)-1.根据你的判断,B 的合理表达式应为( ).

解析 高中阶段学生无法依据所学物理知识及题目信息推导出该题的表达式,但我们可以根据所学公式

,得到磁感应强度B 的单位为Wb·m-2,将真空中磁导率的单位代入题中4个选项,发现A、B、D 三个选项不符题意,只有选项C 能推导出B 的单位为Wb·m-2.故磁感应强度B 的合理表达式应为选项C.
点评 有些问题不一定要通过计算得出答案,我们可以通过量纲分析判断哪些是错误的,这对于解答选择题极有帮助.量纲分析法是一种解决物理、化学和工程等问题的方法,它可以通过分析问题中的物理量的量纲关系,将问题简化,较为准确地估算出某些物理量的关系,量纲法属于定性和半定量分析方法.
例10 (2010年福建卷)物理学中有些问题的结论不一定必须通过计算才能验证,有时只需要通过一定的分析就可以判断结论是否正确.如图6所示为两个彼此平行且共轴的半径分别为R1 和R2 的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1 和O2 相距为2a,连线的中点为O,轴线上的A 点在O 点右侧与O 点相距为r(r<a).试分析判断下列关于A 点处电场强度大小E 的表达式(式中k 为静电力常量)正确的是( ).
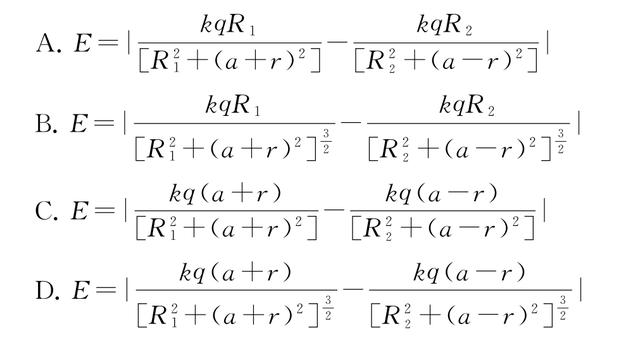

图6
解析 本题若用常规解法推算结果较为烦琐,故而我们可以尝试换一个思路,采用特殊方法进行解答,首先由点电荷场强公式

,得出场强E与k、Q、r2 有关,发现A、C两个选项不符题意.当r 无限接近a 时,即r≈a 时,右侧圆环在A 点产生的磁场强度接近于零,则此时A 处场强只有左侧电荷产生,此时的场强表达式只有一项,排除选项B,故本题选项D 正确.
点评 本题还可以从很多方面进行估算排除选项.物理某些选择题的表达式,有时根据学生已有知识很难推导出结果、甚至于根本行不通.这时我们可以考虑换一个思路,看看其单位是否正确,或者对某些量赋以特殊值代入,对一些未明的数据或表达式作出合情合理的假设,合理近似,科学推理.
估算法是一种常用的科学思维和计算方法,教师要多对学生进行有效引导,指导学生认真审题,创设相应的物理情境,充分挖掘题中的隐含条件,建立合理的物理模型,再利用相应的物理规律进行求解.
(完)
