一道名校小升初几何题，劝退无数学生和家长，少见的几何难题。 如图所示，一个正方形边长是8，两个等边三角形，求阴影部分面积？ 有的同学尝试作垂线利用三角形面积公式解答，也有的同学尝试旋转三角形，其实这道题最简单的思路是延长线段，因为题目给出了特殊角度。#几何问题探讨# #五年级几何题#
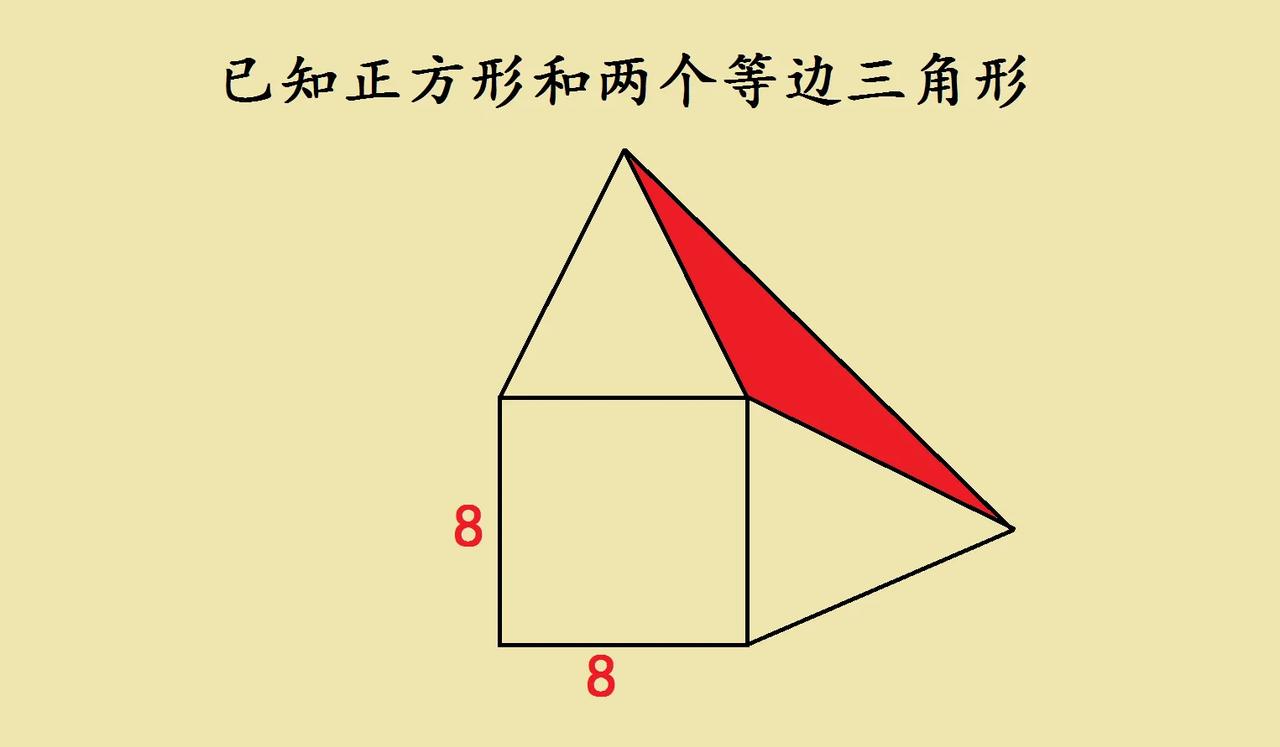
一道名校小升初几何题，劝退无数学生和家长，少见的几何难题。 如图所示，一个正方
大力小学数学吖
2024-11-06 11:18:02
0
阅读：425
用户10xxx48
=16，但是小学学过√没有？
用户10xxx58
阴影也是等腰三角形，顶角是150度，将一条腰边延长与等边三角形一边相交的时候，补角是30度，正好是60度内角的一半，所以腰边延长线才跟等边三角形的一边垂直，角平分线、中线、高三线合一；但也可以直接用公式，两条腰边8*8*中间夹角的正弦值（sin150度=sin30度=1/2），最后再除以2，就是16了
子鱼
以阴影三角形边对折180度，把三角形折到正方形和等边三角形内部，8*4/2=16
曹国清
8*4/2=16
路漫漫
S阴＝½×8×4＝16，隐影三角形随便选择一钝角边延长，与等边三角形相交，容易证明是垂直的，角度是三十度，所以高就是½×8，底边是8
用户10xxx48 回复 11-06 19:33
嗯，对的，我倒是没有考虑到。直接用钝角三角形8的边乘以三角形一半这个高[捂脸哭]
喂，是你
哪两条等边
路漫漫
S阴＝½×8×4＝16，隐影三角形随便选择一钝角边延长，与等边三角形相交，容易证明是垂直的，角度是三十度，所以高就是½×8，底边是8
JYYX
连接最高顶点到右下的角，等到一个等腰三角形。又两个阴影部分面积的对称三角形和全等三角形组成。三角形的高刚好是上面等边三角形右边延长线。根据三角形面积公式 2S=1/2✘8✘8 所以阴影部分面积为16。