难哭全班同学的几何题目,很多学生包括家长根本不会求阴影部分面积。 如图所示,求阴影部分面积? 给出两个长方形面积,又给出了线段长度,我们不妨补充图形,利用长方形面积关系去分析问题,大家可以试试难度如何。
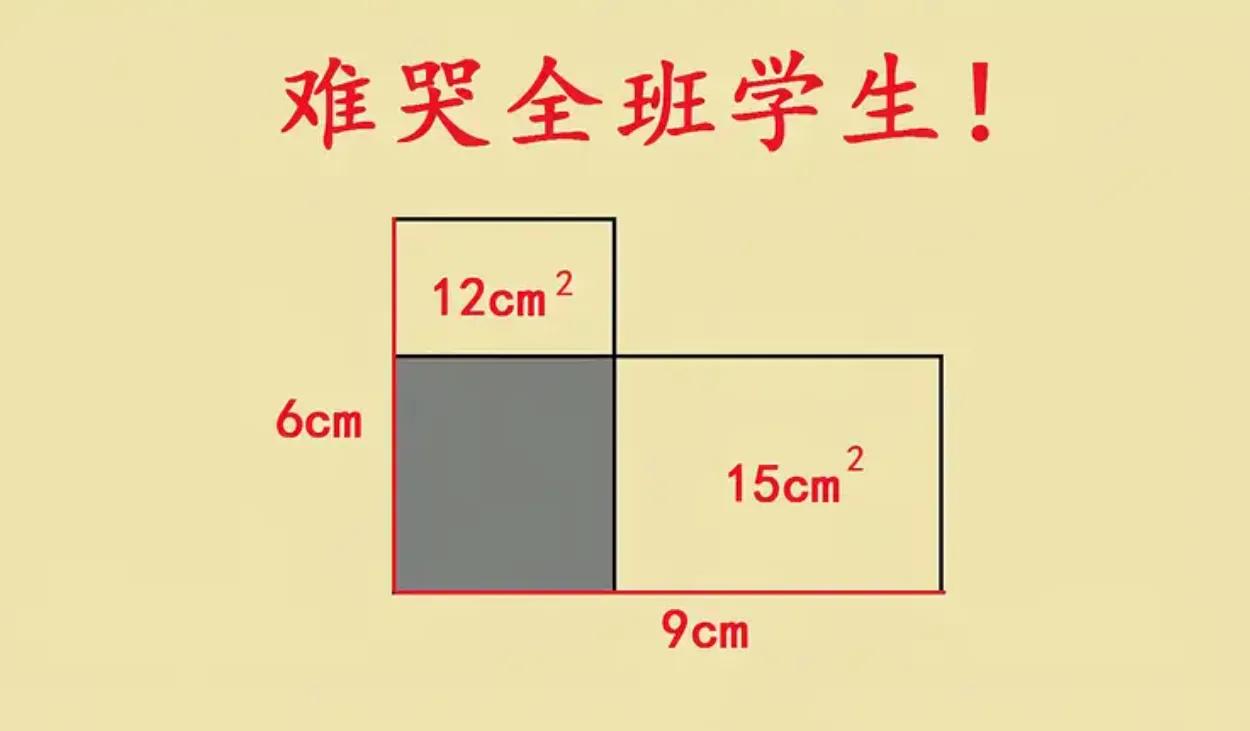
补全大正方形,设阴影部分和另外新的矩形面积为 x,y.容易得到 x+y=6✘9-12-15=27 根据共边得到面积比 x/12=15/y 也就是 x✘y=12✘15 很明显 x=12或者15。
列方程求解阴影矩形a,b边长。面积为12或15
设面积12那块矩形边长为a,b 则ab=12, (9-a)(6-b)=15 6a+9b=54-15+ab=51 2a+3b=17 a=4,b=3 阴影面积为a*(6-3)=12

尧尧2167
12或15。因为已知两个矩形的面积之和(27)正好等于大矩形面积(54)的一半,所以给出的三个小矩形的共同点必定在最大矩形长或宽的垂直平分线上。当这个共同点在长的垂直平分线上时,S阴=15,当这个共同点在宽的垂直平分线上旪,S阴=12。
尧尧2167 回复 11-15 18:02
证明:补全最大矩形右上角的小矩形,设其中间的“十”字分割4线段分别长a、b、c、d,则有ab+cd=27,ad+bc=27,两式左右两边分别相减后得到(a-c)(b-d)=0,所以a=c或b=d。
差池其羽
可以试数,短边是6,假订为3十3,面积12一边为4,阴面积是12,9一4=5,缺面积为3X5=15,12十12十15十15=54=6X9,所以阴面积是十二
用户48xxx25
12
JYYX
补全用两面积做未知量更好求解。
濂溪子
错了
用户12xxx34
补全大长方形就可以求出。
亚楼
把大长方形补齐,则大长方形面积为54,已知面积刚好是27,连接已知长方形对角线,将在一条直线上。由此可知,阴影面积与已知两长方形矩面积和的一半为大长形的一半,所以阴影面积为大长方形面积一半减去已知面积的两长方形一半,即54/2-(12+15)/2=13.5
濂溪子 回复 01-13 23:04
错了
用户10xxx42 回复 12-27 22:11
你这根本不对,你怎么证明俩长方形对角线是一条直线?我假设上面长方形为3×4=12,下面长方形为3×5=15。3+3=6,4+5=9完全符合要求,但阴影面积为3×4=12。
MADAO
有两个解 12或者15 都成立
秋风秋雨zwc
正解,此图画的没有按实际比例。大家以为阴影部分那一块会大一点,实际上就是补全矩形上下中间平分,左右四五分。有两个答案的都是错的。
流水哥哥
用眼看也知道答案是多少了吧!