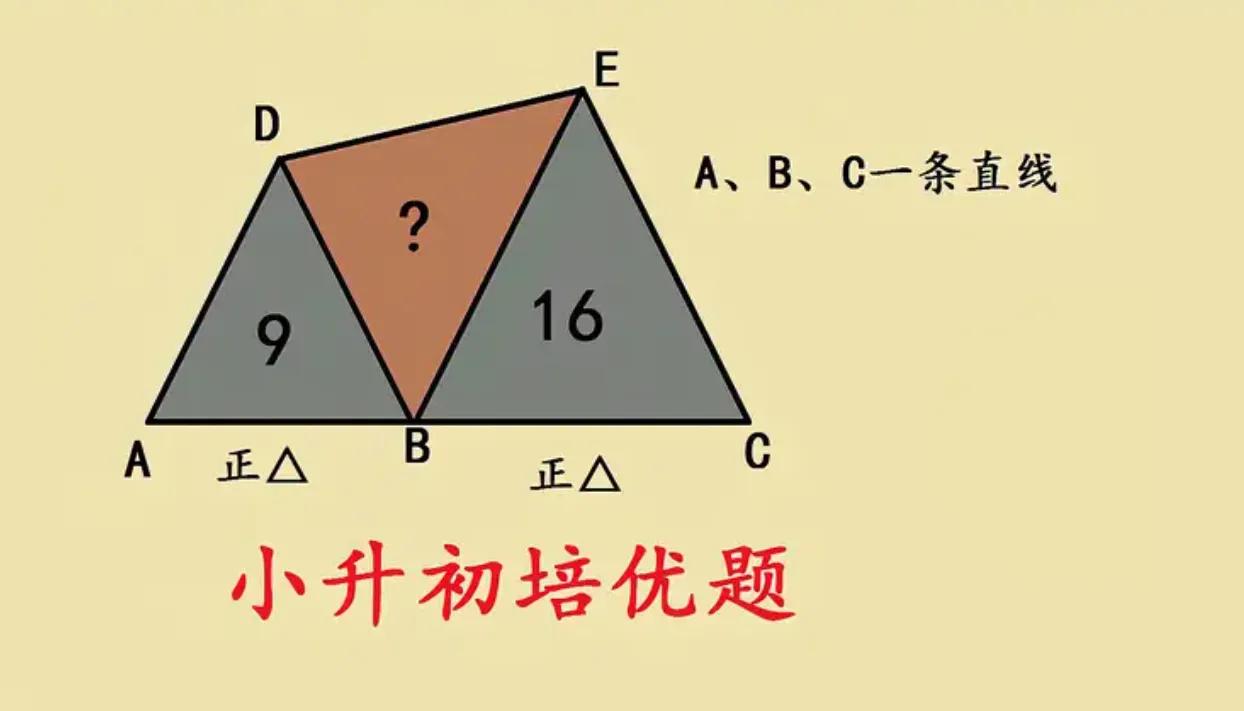
这绝对是小学几何的天花板，经典的求阴影部分面积，很多学生一点思路也没有，因为等边

大力小学数学吖 2024-11-29 12:44:59

这绝对是小学几何的天花板，经典的求阴影部分面积，很多学生一点思路也没有，因为等边三角形知识点小学阶段遇到的很少。如图所示：两个等边三角形面积是9和16，求阴影三角形BDE的面积？这道题难度很大，需要想办法再去构造出一个等边三角形，然后利用三角形相似模型去解题，通过面积比找出线段比，这道题需要用割补法求三角形面积，把阴影三角形分成多个部分去思考问题。几何问题解析

0 阅读：386

评论列表

我的UC 7

2024-12-05 04:23

12。连接AE，阴影面积等于三角形ABE面积。阴影面积是9×4/3=12
用户10xxx48 3

2024-11-29 19:58

12？

喂，是你回复:

12是错的，AB≠3

12-05 01:47

用户10xxx48 回复: 喂，是你

没说AB：BE＝√（9：16）=3：4.相似三角形的面积比是对应边长比的平方这个定律。

12-05 04:36
喂，是你 2

2024-12-05 01:15

分别过D点E点作AC的垂线，相交AC于点F点G，据海伦公式可知：AB=3 DF=6，同理：BC=4 EG=8,S阴=S梯形DFGE减去已知两个正三角形面积的一半，即：(6+8)*(3+4)/2/2-(16+9)/2=12
JYYX 2

2025-01-04 08:39

文章不是提了一句等边三角形么？把AD,AE延长相交与H，就是一个大的等边三角形，然后它由两个小等边三角形和两个全等三角形组成。根据相似比，得出边长3:7，所以面积49。（49-9-16）/2=12