两极分化:有的孩子用时不到10秒、就口算出答案,有的孩子折腾半天、仍无头绪,甚至还认为题目错了或缺少条件!这是一道小学五年级数学竞赛题:大正方形边长及面积均未知,咋求阴影面积? 如图,两个正方形并排摆放在一起,小正方形ABCD的面积为6,大正方形CEFG边长及面积均未知,连接BF、与CD相交于点M,求红色阴影部分四边形ADFM的面积。 —————————— 提示:等积原理(同底等高三角形面积相等)! ①连接BD,则S△ADM=S△BDM,从而S阴影=S△BDF。 ②连接CF,则AD⫽CF,从而S△BDF=S△BCD=1/2S正方形ABCD。这道题可以通过连接对角线,通过三角形面积关系进行等积转换,然后把阴影部分面积想办法转换为已知图形面积。 友友们,怎么看?欢迎留言分享! 小学数学
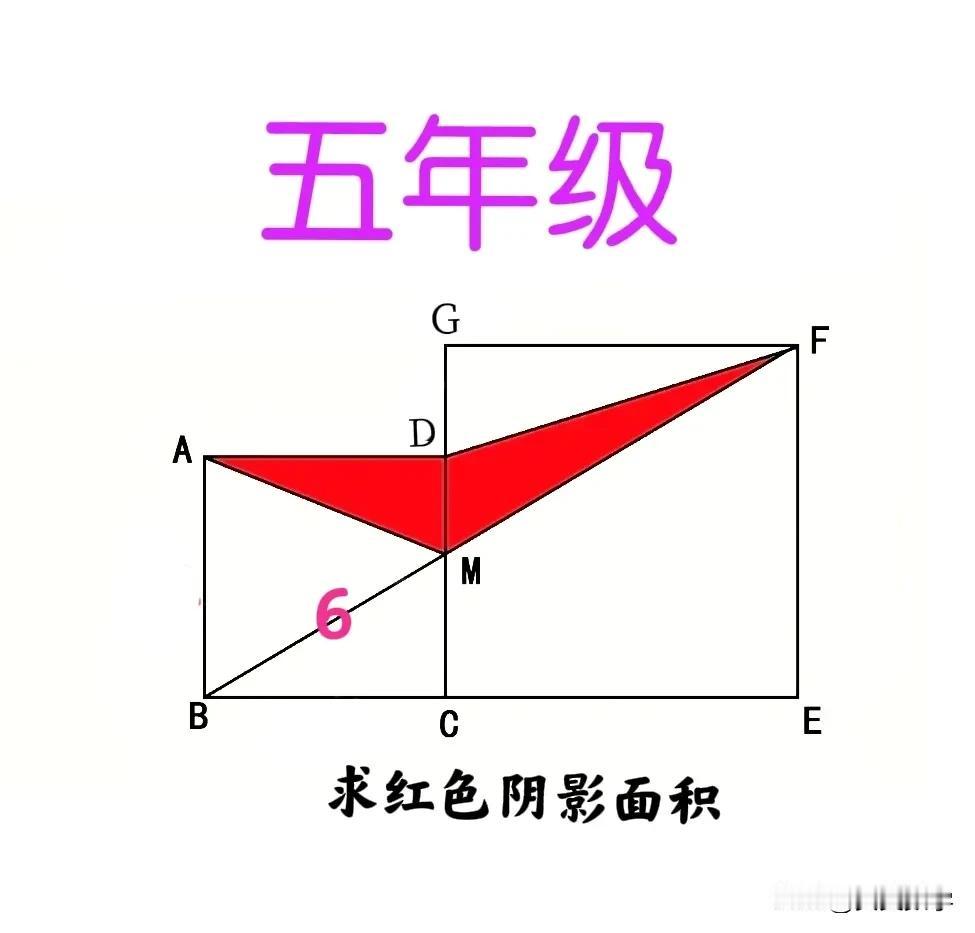





连接BD和CF,BD//CF,根据同底等高或蝴蝶模型,S三角形BCM=S三角形DMF,S阴=S三角形ADM+S三角形BCM=1/2小正方形=6//2=3
三角形的面积公式是低乘高除二。那大三角形如果是无限大,那怎么确定阴影的面积?
连接BD、CF,由于DB∥CF(同位角均为45°),形成梯形BCFD,根据等底等高原理,S△ADM=S△BDM,根据蝴蝶定理,S△DFM=S△BCM,∴S四边形ADFM=S△BDC=1/2*6=3。