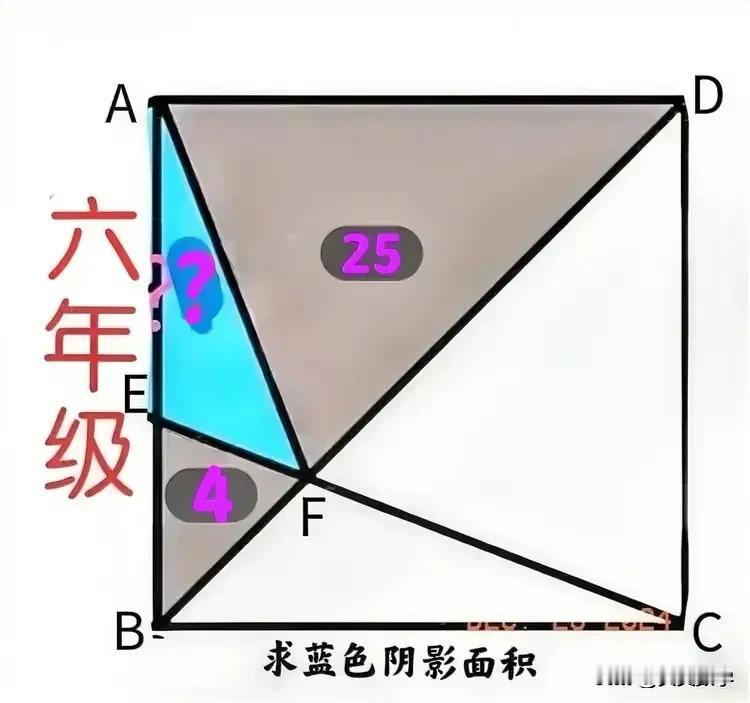
“会的几乎没有，个别尖子生除外！”这是一道小学六年级数学竞赛题：三边均未知，咋求三角形面积？ 如图，点E在正方形ABCD边AB上，连接BD和CE，相交于点F，三角形ADF和BEF的面积分别为25和4，求蓝色阴影部分面积。 ————— 提示：对称性+等高三角形面积比等于底边之比！适合小学生 ①点F在正方形ABCD对角线BD上，由对称性可知S△CDF=S△ADF=25。 （这点比较容易说明，过点F分别作AD和CD的垂线FM和FN，则DMFN为长方形，DFM和DFN均为等腰直角三角形，故DMFN为正方形，且FM=FN，从而S△CDF=S△ADF。） ②连接DE，由同底等高三角形面积相等可知，S△BDE=S△BCE，从而S△DEF=S△BCF。 ③由等高三角形面积比等于底边之比可知，S△DEF/S△BEF=DF/BF=S△CDF/S△BCF，也即S△DEF×S△BCF=S△BEF×S△CDF=100，从而S△DEF=S△BCF=10。 ④同于步骤①，由对称性可知S△ABF=S△BCF=10，故S△AEF=S△ABF-S△BEF=10-4=6。 提示二：三角形相似+相似三角形面积比等于相似比的平方！适合初中生 ①同于提示一，可知S△CDF=S△ADF=25。 ②由△BEF~△DCF，可得(EF/CD)²=S△BEF/S△CDF=4/25，故EF/AB=EF/CD=2/5，从而S△BEF/S△AEF=BE/AE=2/3，也即S△AEF=3/2×4=6。 友友们，怎么看？欢迎留言分享！