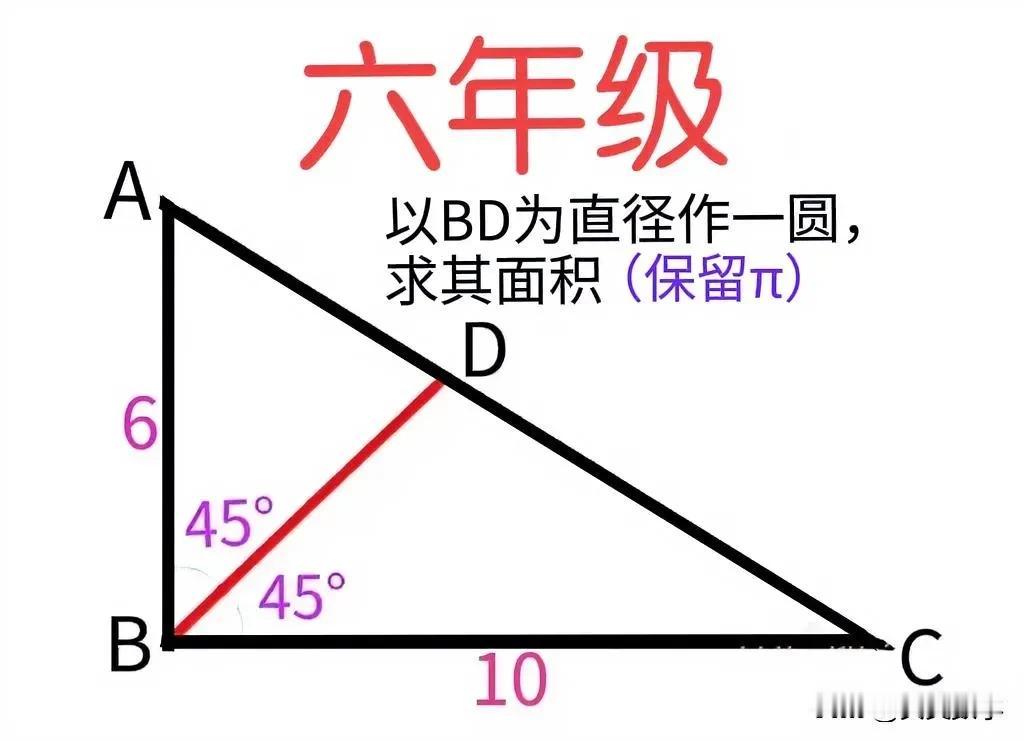
“会的寥寥无几,正确率不到5%!”小学六年级数学拓展题型:半径未知且无法求出(实为无理数),咋求圆的面积? 如图,直角三角形的两直角边长分别为6和10,D为斜边AC上一点,∠ABD=∠CBD=45°,以BD为直径作一圆,求其面积(保留π)。 难点:直径BD无法求出、实为无理数! 切入点:求BD²! ———————— 提示:先求BD²! ①过点D分别作AB与BC的垂线DE和DF,则BEDF为正方形、其对角线为BD。 ②30=AB×BC÷2=S△ABC=S△ABD+S△BCD=AB×DE÷2+BC×DF÷2=8×DE,从而DE=15/4。 ③正方形BEDF可由2个等腰直角三角形BED拼成、以BD为边长的正方形可由4个等腰直角三角形BED拼成,故DE²=S正方形BEFD=BD²÷2,从而BD²/4=DE²/2=225/32。 ④r²=BD²/4,故S圆=225π/32。 友友们,怎么看?欢迎留言分享!