斯坦福华人博士生打破58年僵局，牛顿提出的亲吻数问题有了新突破牛顿想出的“球

斯坦福华人博士生打破 58 年僵局，牛顿提出的亲吻数问题有了新突破

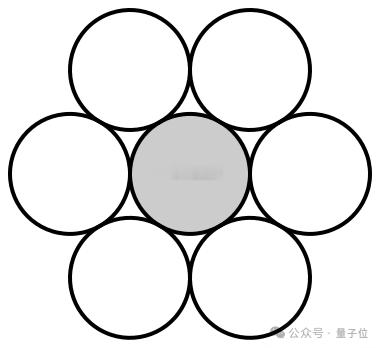
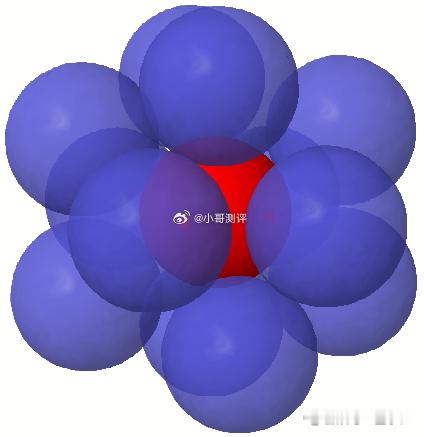
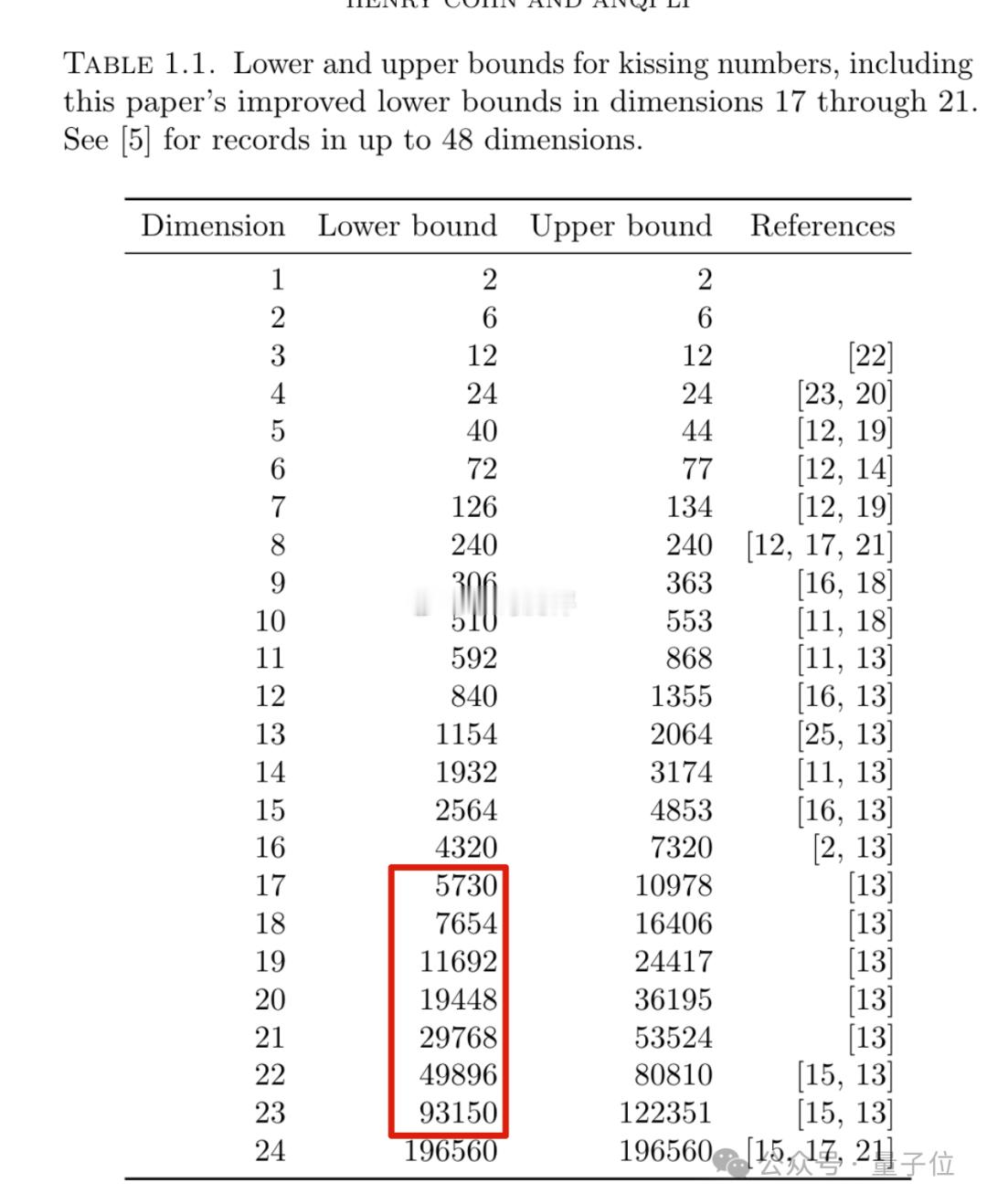
牛顿想出的“球体亲吻数”（kissing number）难题，华人学者取得新进展。n 维空间中，给定一个 n 维球体，最多有几个相同的球体可以与它接触而不重叠？

斯坦福博士生 Anqi Li 在微软实习期间完成这项研究，导师 Henry Cohn 本意是让她用计算机辅助，她却创造性地找到了数学上的新解法。

另外，这个问题还与通信领域的编码纠错问题密切相关，曾被 NASA 用来设计旅行者号探测器的通信编码：使用 24 位二进制编码，仅需一个灯泡的功率（约 20 瓦），就将彩色照片从太空传回地球。

那么，二进制编码与高维球体是怎么联系起来的？如果将每个通信编码看做高维空间中的一个点，这个点也可以被视为一个球体的球心。

此时球的半径就代表了容错的范围，当传输过程中出现噪声导致信息失真时，接收到的信息会偏离原始编码。但如果失真后的信息仍落在某个编码词对应球体的范围内，就可以识别出原本要传输的编码，这就实现了通信中的错误纠正。

至此，通信编码设计问题就转换成了求解高维空间中球体堆砌问题，而亲吻数问题正是研究局部最优堆砌的重要工具。

反过来也成立，编码设计的进步也能帮助数学家改进高维亲吻数问题的结果。