人们普遍认为在车祸中越大的车会越安全。
表 12-1 列出了在汽车碰撞测试中不同车型对头部损伤测量的结果(数据来自数据集 35“汽车碰撞数据”)。

头部损伤是车祸中造成人员死亡和致残的主要原因。
在汽车碰撞测试中,头部损伤结果是根据“头部损伤标准”(Head Injury Criterion,HIC)来衡量的。
HIC 被用来衡量撞击造成头部损伤的可能性。HIC 值越大,在车祸中造成头部损伤的概率就越高。
在介绍统计方法之前,我们应当先探索一下数据。样本统计数据如表 12-2 所示。

参考数据的统计量以及不同车型 HIC 的箱形图。非正式的比较表明,小型车的均值高于其他类型的车。但箱形图中四类车的数据有所重叠,所以差异并不明显。因此,我们需要使用统计方法来判断差异是否显著。
我们可以使用《基础统计学》一书 9-2 节介绍的两个总体均值差的检验方法,但是该检验需要进行两两比较, 而这里的样本来自四个不同的总体。当有来自三个或三个以上总体的样本时,通常使用方差分析 (Analysis of Variance,简称 ANOVA)方法以检验总体均值是否相等。
核心概念:使用双因素方差分析方法,我们需要先根据两个因素将数据分为两类,然后检验两个因素之间是否存在交互作用,最后检验两个因素是否分别具有主效应。
表 12-4 中包含了在汽车碰撞测试中测得的股骨受力数据(千牛顿)。该表根据以下两个因素进行分类。
1. 股骨部位:左腿股骨或右腿股骨。
2. 车型:小型车、中型车、大型车、SUV。

表 12-4 中的每个子分类都被称为单元,所以该表中有 8 个单元,每个单元中各有 5 个值。
当然,我们可以根据车型或者股骨部位分别进行单因素方差分析,但该方法忽略了一个重要特征:两个因素之间可能的交互作用。
定义
如果一个因素对结果的影响依赖另一个因素中不同的类型,那么这两个因素之间存在交互作用(或称为交互效应)。
作为两个因素之间交互作用的例子,可以考虑食物搭配。花生酱和果冻搭配所产生的交互作用就很好,但番茄酱和冰淇淋搭配所产生的交互作用会导致口感不佳。一般来说,把交互作用看作是由于两个因素的结合而产生的效应。
均值与交互图
计算表12-4 中每个单元的均值(见表 12-5)并作图(见图 12-3)。每个单元的均值从 0.68 到 1.02 不等,可以看出均值间存在明显的差异。我们称图12-3为均值交互图,并可以通过如下方法进行解读。
交互作用:如果线段之间明显不平行,则可能存在交互作用。无交互作用:如果线段之间近似于平行,则可能不存在交互作用。

由于依赖表 12-5 和图 12-3 做出的判断过于主观,我们还是需要更为客观的方法来判断两个因 素之间是否存在交互作用,即使用双因素方差分析方法。参考以下“关键要素”。
关键要素
双因素方差分析
目标
双因素方差分析:①检验两个因素之间是否存在交互作用。②检验两个因素是否分别具有主效应。
条件
1. 对于每个单元,样本值近似服从正态分布。
2. 各总体的方差 σ 近似相同。
3. 样本为随机选取的数据。
4. 样本间相互独立。
5. 样本值可被分为两类。
6. 所有单元内样本值的数量相等(该条件称为平衡设计)。
双因素方差分析流程(见图 12-4)
假设两个因素分别为因素 A 和因素 B。
步骤 1 交互作用:原假设为两个因素之间不存在交互作用。通过统计软件计算以下检验统计 量以及相应的 p 值。
其中, 被称为误差均方(Mean of Squares Due to Error), 被称为交互项均方(Mean of Squares Due to Interaction)。根据以下准则做出判断。
p 值≤ α:拒绝原假设,两个因素之间存在交互作用。p 值 >α:不能拒绝原假设。步骤 2 主效应:如果在步骤 1 中发现两个因素之间存在交互作用,则跳过此步骤。如果得出两个因素之间不存在交互作用的结论,则对每个因素分别检验其主效应。以因素 A 为例,该检验的原假设是因素 A 没有主效应(即检验因素 A 下所有的样本是否来自均值都相等的总体)。通过统计软件计算以下检验统计量以及相应的 p 值。
其中, 被称为因素A均方(Mean of Squares Due to A)。
根据以下准则做出判断。
p 值≤ α:拒绝原假设,因素 A 具有主效应。p 值 >α:不能拒绝原假设。例 1:

例:汽车碰撞测试中的股骨受力情况
给定表12-4中的数据:①检验两个因素之间是否存在交互作用,其中一个因素为车型(小型车、中型车、大型车、SUV),另一个因素为股骨部位(左腿股骨、右腿股骨)。②分别检验两个因素是否具有主效应。(取 α=0.05)
解答:
检查条件:①根据正态分位图,大部分单元内的样本值近似服从正态分布。右腿股骨 / 小型车和右腿股骨 /SUV 单元内的样本也能通过正态性检验(取 α=0.01)。②各单元的方差并不相等,但该检验对偏离齐方差具有鲁棒性。③根据研究设计,可以将样本视为简单随机样本。④样本间相互独立。⑤样本值可被分为两类:股骨部位和车型。⑥所有单元内的样本量都为 5。所有条件都满足。
以下是 StatCrunch 的双因素方差分析结果。
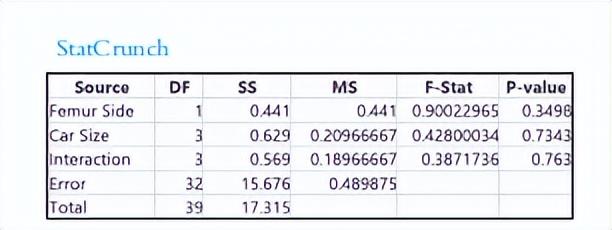
步骤 1 交互作用:StatCrunch 的分析结果显示 F=0.3872。该值可通过上图中的另外两个值计算得到。

其对应的 p 值为 0.763,因此我们不能拒绝原假设。股骨受力情况并不与股骨部位和车型的交互作用有关。
步骤 2 主效应:因为没有发现存在交互作用,所以分别检验两个因素的主效应。这里以股骨部位为例,其对应的原假设是股骨部位没有主效应(即股骨部位的样本来自均值相等的总体)。
参考StatCrunch 的分析结果,显示 F =0.9002。该值可通过上图中的另外两个值计算得到。

其对应的 p 值为 0.3498,因此我们不能拒绝原假设。股骨受力情况不会受是左腿股骨还是右腿股骨所影响。类似地,检验另一个因素的主效应,可以得出股骨受力情况也不会受车型所影响的结论。
解读:
根据表 12-4 中的样本数据,可以得出结论:股骨受力情况不会受股骨部位(是左腿股骨还是右腿股骨)和车型所影响,也不会与股骨部位和车型之间的交互作用有关。
注意:双因素方差分析并不是重复两次单因素方差分析,因为它需要检验交互作用。
使用软件
双因素方差分析
Excel(需要 Excel 加载项:分析工具库)
在创建数据表格时,如果每个单元内有多个样本值(即多次试验),那么同一单元内的样本值按列往下依次列出(不能按行)。每个因素对应的各个类别(标签)都应被输入 A 列和第一行, 参见下表:

1. 点击“数据”选项卡,然后点击“数据分析”。
2. 在“分析工具”下选择“方差分析:可重复双因素分析”,点击“确定”按钮。
3. 在“输入区域”中输入数据范围。
4. 在“每一样本的行数”中,输入每个单元内样本值的数量。
5. 输入所需的 x 值。
6. 点击“确定”按钮,展示结果。
R
R 命令:
方差分析建模:aov(y~x1+x2+x1*x2)
双因素方差分析的额外信息:summary(aov(y~x1+x2+x1*x2))
其中,y 为数据值,x1 和 x2 为对应的分类名称,x1*x2 为交互作用

以上内容摘自《基础统计学(第14版)(双色)》一书!

