题目

不出所料,今年又是课本基础定理的逆向用法
第一问 证中点
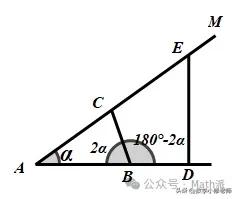
证明一个点是线段中点,思路有很多,如
倍长中线(逆用法)
中位线(逆用法)
Rt△斜边中线(逆用法)
三线合一(逆用法)
我们要选取哪个思路?
看条件暗示
180°-2α→补角2α
2α和BC=BD
常见考法如下

暗示联结CD
考察Rt△斜边中线(逆用法)

易知AC=CD

因为∠ADE=90°
易知∠CDE=∠CED=90°-α
因此CE=CD
可得AC=CE
第二问分析

可以先度量猜猜答案

可以猜测EF=2AC
证明线段2倍关系常见思路
将长的线段截成2半,在证相等
先取EF中点

还会联结哪些线段?看条件暗示
DF∥AN

∠FDE=90°
暗示联结HD(Rt△斜边中线)

HD=HF=HE
第一问+BC=BD
暗示手拉手模型

以B为圆心BA为半径画圆
交AM于点G
可得BA=BG
根据手拉手模型

易知△ABC≌△GBD(SAS)
其中∠ABC=∠GBD(公共角模型)

∠A=∠GFD=α(同位角相等)
∠A=∠AGB=α(等边对等角)
∠A=∠BGD=α(全等对应角相等)
可知
∠DHG=∠HGD+∠HDF=2α
∠DGH=∠AGB+∠BGD=2α
可得
DH=DG
又因为AC=DG(全等对应边相等)
则AC=DG=DH=HF=HE=1/2FE
可得EF=2AC
所以此题就是以下三个小点
手拉手模型
Rt△斜边中线
等腰△
注:以上是分析过程,请同学自己写答题过程。
