理解现代物理，张量是你无法绕过的概念，它推动了物理学的统一

你有没有想过，在现代物理的领域里，还有一个概念是我们无法绕过去的？就像物理学的“恶势力”一样，它不仅仅是一个单纯的数学工具，而是推动了物理学的统一和发展，这个概念就是张量。

张量的神秘和复杂让很多人望而却步，但它也是现代物理学不可或缺的一部分，它帮助我们更深入地理解物理世界的本质，张量背后的数学和物理深度更是令人敬畏。

一、张量的起源：拉伸的意思，张量就是高维空间中的“拉伸”

张量这个名字源于拉丁词“拉伸”，张量就是高维空间中的“拉伸”这个概念。张量可以看作是一个多维数组，它的每一个维度对应一个物理量，而这些物理量之间的关系则由张量的具体形式来表示。

在某种意义上，张量就像是高维数列的一个扩展，它可以在高维空间中描述物理量之间的关系，比如我们在定义物体的刚性时，可能需要引入一个称为刚度张量的量，它就是通过拉伸定义的。

二、张量的身份：描述物理现象的关键工具

(1)张量的定义，变换坐标时保持物理意义不变

那么，张量是什么呢？简单来说，张量就是一种在变换坐标时保持物理意义不变的数学对象，张量的定义比较抽象，但可以通过以下两个方面来理解：

第一，张量的变换规则。张量在坐标变换下的变化规律叫做“变换规则”，它是张量的核心特征之一，例如，如果一个物理量在某一坐标系下被表示为一个张量 T，在另一个坐标系下它可以通过一定的变换规则重新表示为一个新的张量T'，但物理现象的本质不会因为坐标系的不同而有所变化。

第二，张量的几何表示。每个张量都有其对应的几何对象，张量的阶数（也称为张量的维度）和张量的维度是两个独立的概念，比如零阶张量是标量，一阶张量是向量，二阶张量有时也称为矩阵，它在三维世界中相当于一个立体，三阶和更高的张量就有点复杂了，需要同时考虑到多个维度的变换，涉及到很多复杂的计算。

因此，在实际应用中，我们通常不会涉及超过三阶的张量，大多数物理学家和工程师只需要处理零阶到二阶张量，比如电场强度是二阶张量，电荷是零阶张量。

(2)张量在物理中如何体现？看这几个例子

①应力张量

在物理学中，张量的应用非常广泛，其中一个重要的应用就是在描述物体在不同方向上受到的力的分布情况，这时，就需要用到一种特殊的张量，称为应力张量。应力张量是一种二阶、三维张量，它描述的是在一个材料内部任意一点上，由外界施加的压力或拉力分布情况。

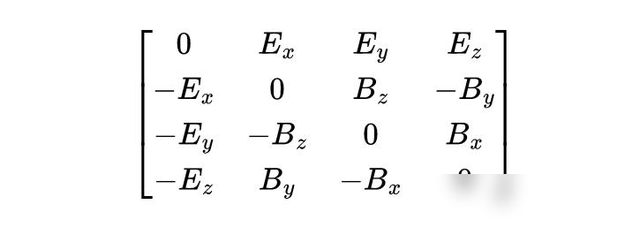
应力张量包含了材料的弹性性质和变形行为等信息，是力学分析中不可或缺的工具。对于一个立方体，我们可以用一个三维的立方体来表示它的受力情况，每个面上的箭头表示力的大小和方向，张量的三维性也反映出了物理量的多维性，力不仅可以用三维向量表示，实际上它的影响还可能是多维的，量子物理中粒子的自旋就是一个典型的例子。

②电磁场张量

电磁场张量是描述电磁场的一个重要工具，它是一个四维的张量，通过它可以快速方便地计算出各种电磁场的物理量，如电场强度、磁场强度等。电磁场张量是一个四维张量，它包含了电场和磁场的信息，是描述电磁场的一个重要工具。

在经典力学中，电场和磁场是两个独立的物理量，但在相对论中，它们被统一为一个四维张量，通过电磁场张量，我们可以更方便地计算电磁场的各种物理量，如电场强度、磁场强度等，在量子物理中，电磁场张量也有重要的应用，如粒子的相互作用和辐射等。

电磁场张量的全称是法拉第张量，四个分量分别为：电场强度E的分量Ex，Ey，Ez和磁感应强度B的分量Bx，By，Bz。在四维时空中，法拉第张量可以用一个 4×4的反对称张量来表示，这个形式就像左侧这个表格一样，四维电磁场张量的分量在坐标变换下是这样变化的，如法拉第张量的分量Fμν在洛伦兹变换下的变化规律就是：F'μν = LμLνFαβ，这个性质就是张量的定义。

③真正的向量VS伪向量，区别在这里

在物理学中，通常将矢量称为“真正的向量”，而将物理意义上和真正的向量类似的量称为“伪向量”，伪向量和真正的向量的主要区别在于坐标系的改变如何影响它们的物理意义。

当我们将一个真正的向量从一个坐标系转移到另一个坐标系时，它的物理意义是不变的，比如速度就是一个真正向量，速度的定义就是： v = dx/dt，dx是物体在时间t到t+dt之间的位移，其方向和大小是不变的。而伪向量在坐标系之间的转移时，可能会出现反向变换，导致其物理意义发生变化。

例如，在经典力学中，物体的角动量就是一个伪向量，在静止坐标系下物体的角动量是L = r × p，物体以等速度平移时，角动量的值并不会发生变化，但其方向会因坐标系的不同而不同；而速度作为一个真正的向量，则不会因坐标系的转移而改变其大小和方向，以向量形式表示为 v = (vx,vy,vz)，vx，vy，vz的符号都是不变的。