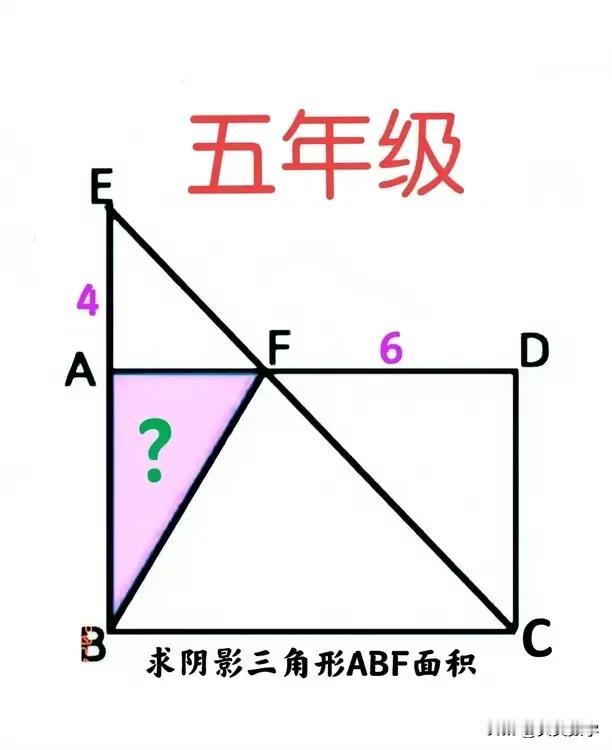
“几乎都不会，个别尖子生除外！”有人说条件不够（比如长方形的长与宽均未知）无法求

“几乎都不会，个别尖子生除外！”有人说条件不够（比如长方形的长与宽均未知）无法求解，有人说不用已知长方形的长与宽！这是一道小学五年级数学竞赛题：三边全都未知，咋求三角形面积？ 如图，ABCD为长方形，延长BA至点E，连接CE、与AD相交于点F，AE=4，DF=6，求阴影部分三角形ABF的面积。 ———————— 提示一：同底等高三角形面积相等！ ①连接AC，则S△ABF=S△ACF。 ②连接DE，则S△ACE=S△ADE，从而S△ACF=S△ACE-S△AEF=S△ADE-S△AEF=S△DEF=AE×DF÷2=12。 提示二：补齐长方形+对角线平分长方形面积！ ①作一以AE和BC为边的长方形ACGF：过点E作CD延长线的垂线EG即可。 ②过点F作BE的平行线，分别与BC和EG相交于点M和N。 ③由对角线平分长方形面积可知，S长方形ABMF=S长方形DGNF，从而S△ABF=1/2 S长方形DGNF=12。 妙笔生花创作挑战 小学数学

不能用相似全等真难受，设长方形的长为x，宽为y,因为s△ebc＝s△efb+s△bfc ,所以得出方程4+y的和乘以x＝x-6的差乘以y+4的和+xy，最后得出24＝x-6的和乘以y，x-6和y分别是△abf的直角边，所以答案是12。