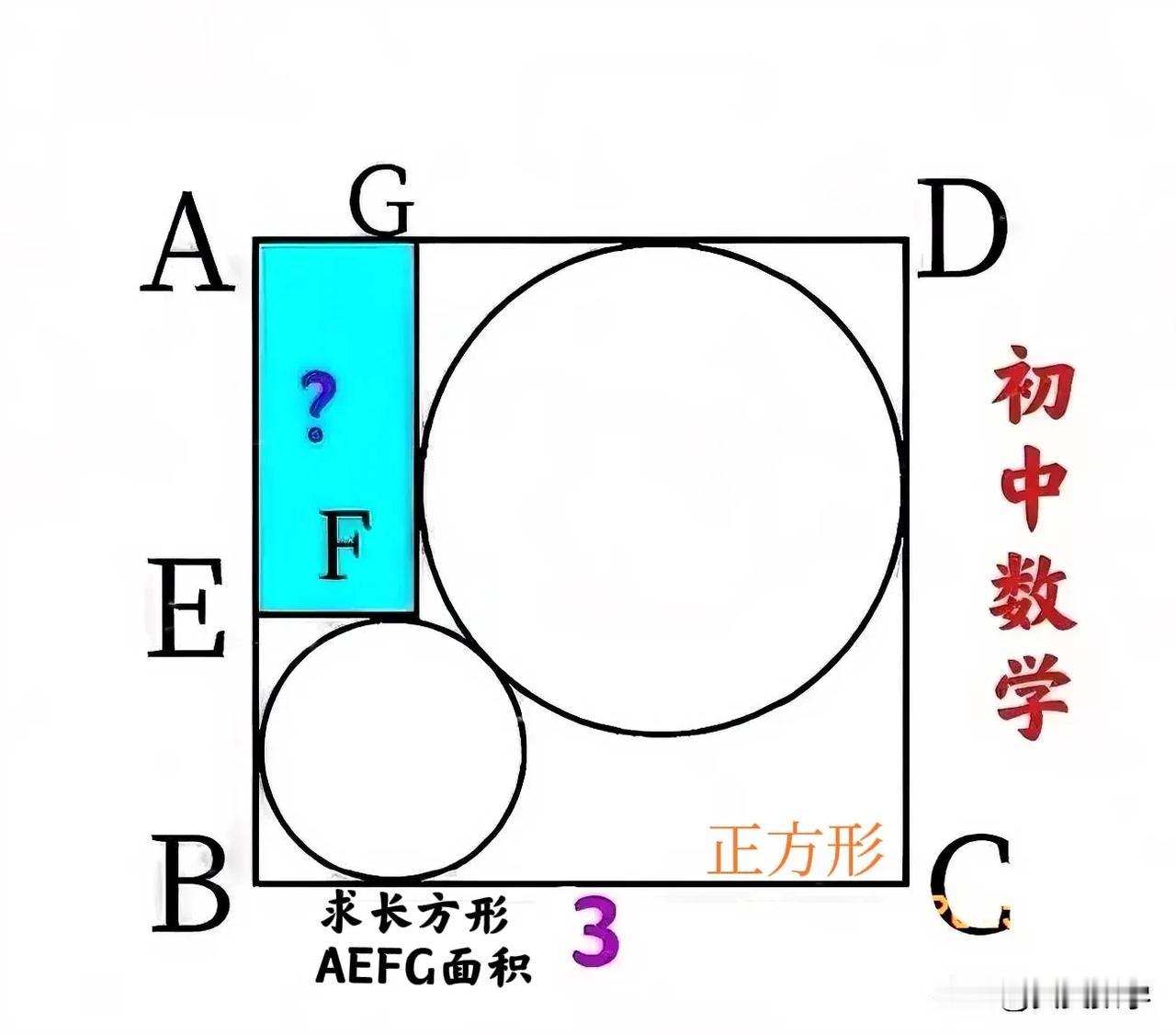
“正确率不足5%，交白卷的倒不少！”很多同学抱怨，示意图没标出圆心、这使得他们一时找不出边角关系，只好交白卷！这是一道初中三年级数学题：主要考查勾股定理及相切圆的性质！ 如图，正方形ABCD的边长为3，在其内部有一大一小两个圆，它们的半径之比为2 : 1，长方形AEFG的两边分别与这两个圆相切，求长方形AEFG的面积。 解题关键：在示意图中找出恰当的边角关系，并据此求出半径！ ——————— 提示一：从对角线找边角关系！ ①连接BD，那么BD会经过两个圆的圆心，把BD与大圆周、小圆周的交点分别记为M、P（切点）和N。 ②设小圆半径为r，那么BN = (√2×2r - 2r)/2 = (√2 - 1)r，DM = (√2×4r - 4r)/2 = 2(√2 - 1)r，所以BD = BN + DM + 6r = 3(√2 + 1)r = 3√2，进而得出r = 2 - √2。 ③S长AEFG = (3 - 2r)(3 - 4r) = (2√2 - 1)×(4√2 - 5) = 21 - 14√2。 提示二：从两圆圆心连线找边角关系！ ①分别过小圆的圆心O₁和大圆的圆心O₂作CD和BC的垂线，这两条垂线相交于点H，那么O₁O₂H是等腰直角三角形。 ②O₁H = O₂H = 3 - 3r，O₁O₂ = 3r，并且O₁O₂ = √2O₁H，所以3r = 3√2 - 3√2r，也就是r = 2 - √2。 朋友们，你们怎么看呢？欢迎留言分享！