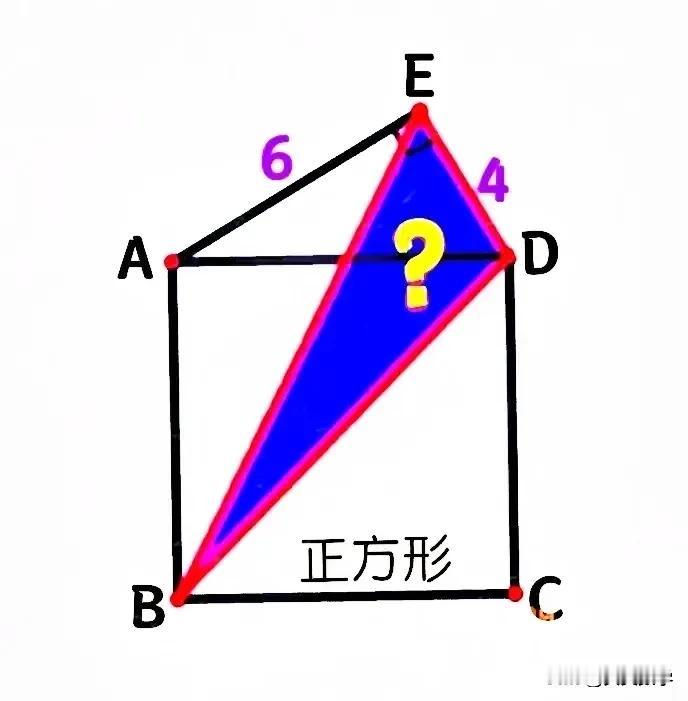
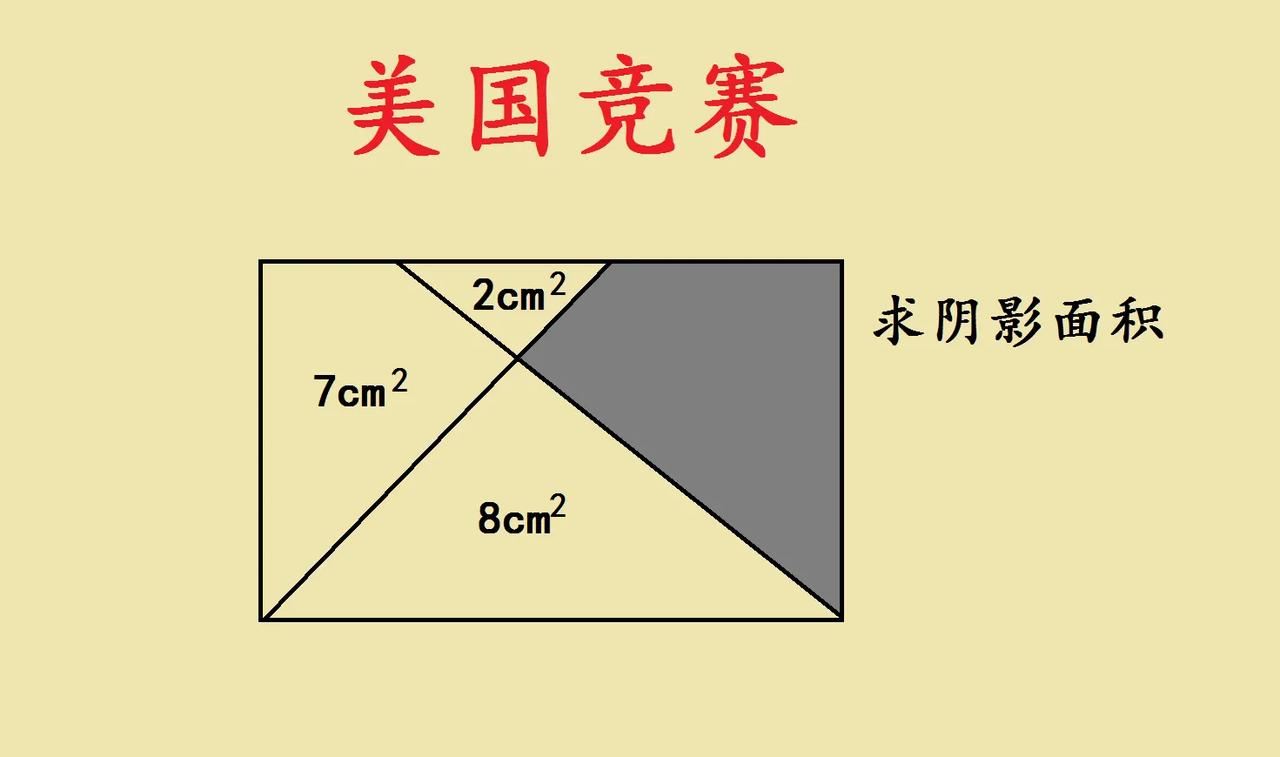
“会做的没几个，交白卷的一大堆！”小学五年级数学竞赛题型：三角形仅一边已知，咋求面积？ 如图，以正方形ABCD的边AD作一直角三角形ADE，AE=6，DE=4，求阴影部分三角形BDE面积。 突破口：构造1个三角形，使得其面积可直接求出、且等于△BDE的面积！ ———————— 提示：拼图（或图形旋转）+等积代换！适合五年级 ①作△ADE的内弦图：用4个与△ADE相同的三角形（按长短直角边交替相连）拼成1个边长为AE+DE=10的大正方形，其中间空白部分恰为正方形ABCD。 或 ①'过点B作EA延长线的垂线BF，将△ADE绕点A顺时针旋转90°至AD与AB重合，旋转后的三角形记为△ABE'，则AFBE'为长方形，故AF=BE'=DE=4，从而EF=6+4=10。 ②BE⫽DE，故S△BDE=S△DEF=10×4÷2=20。 友友们，怎么看？欢迎留言分享！
评论列表
猜你喜欢
【3评论】【4点赞】
【3评论】【3点赞】
【1评论】【27点赞】
【3评论】【3点赞】
【4点赞】
【2评论】【4点赞】
作者最新文章
热门分类
教育TOP
教育最新文章
喂，是你
根据已知条件，可求出AD=2√13,BD=2√26,S四边形ABDE=4*6/2+2√13*2√13/2=12+26=38,设EB为x,根据海伦公式：令(6+2√13+x)/2=a,(4+2√26+x)/2=b,可知(√a*(a-x)(a-6)(a-2√13)+(√b*(b-x)(b-4)(b-2√26)=38,
难能可退
因为没有说明角AED的度数，所以可以假设角AED为180℃，此时AED为一条与AD完全重合的直线，即正方形AD的长度=AE+ED=6+4=10，阴影面积即三角形BED的面积为ED×AB÷2=4×10÷2=20，这才是奥数的算法，化繁为简，考的是想象力和罗辑思维能力