有趣的挂谷问题,平面上一根针转动180度掉头,扫过的面积可以任意小!
昨说了中国女学者可能靠解决三维挂谷问题,获得菲尔兹奖。论文证明过程我看了,开头说问题能明白,但第一个关键想法就懵逼了,数学不会就是不会。
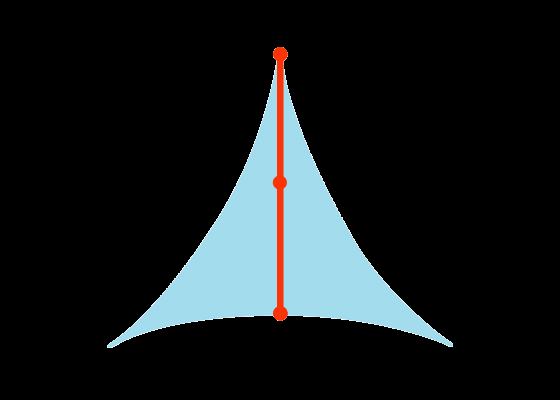
这问题本身,倒是不难懂,小学生都能理解。图一,一根单位长度的针要掉头,会扫过多大面积,最小是多少?这是1917年挂谷宗一提出的问题。
最简单的想法是以线段中点为圆心,转180度,这是一个圆,半径是1/2,面积是π/4。图一是一个改进,叫deltoid,三角旋轮线。线段的一端沿着边行走,这个图形就出来了,面积π/8。能不能继续缩小面积?
真正让人惊讶的结果是,这个面积可以缩小到任意小!苏联学者贝西科维奇1928年找到了办法。
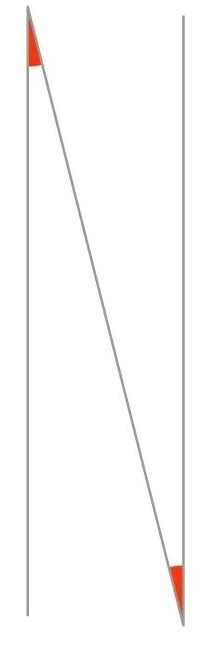
具体办法是让针走N字型,蛇皮游走。图二,针先沿着N的左腿上行,这个动作扫过面积为0。第二步转动扫过一点角度,占一点点面积。第三步沿着斜腿下来,到达下面。第四步,再转动一点角度,一点点面积。第五步,上行。
这个蛇皮游走很精妙,如果N的腿非常长,角度非常小,扫过的面积可以小于任意给定数值。
用多个N字型蛇皮游走,不断组合,就可以让针掉头,而扫过总面积还是小于给定的任意数值。当然这里还有些细节,但精华思想就是这个。
三维问题就有些复杂,论文很难懂。但二维情况是可以理解的。