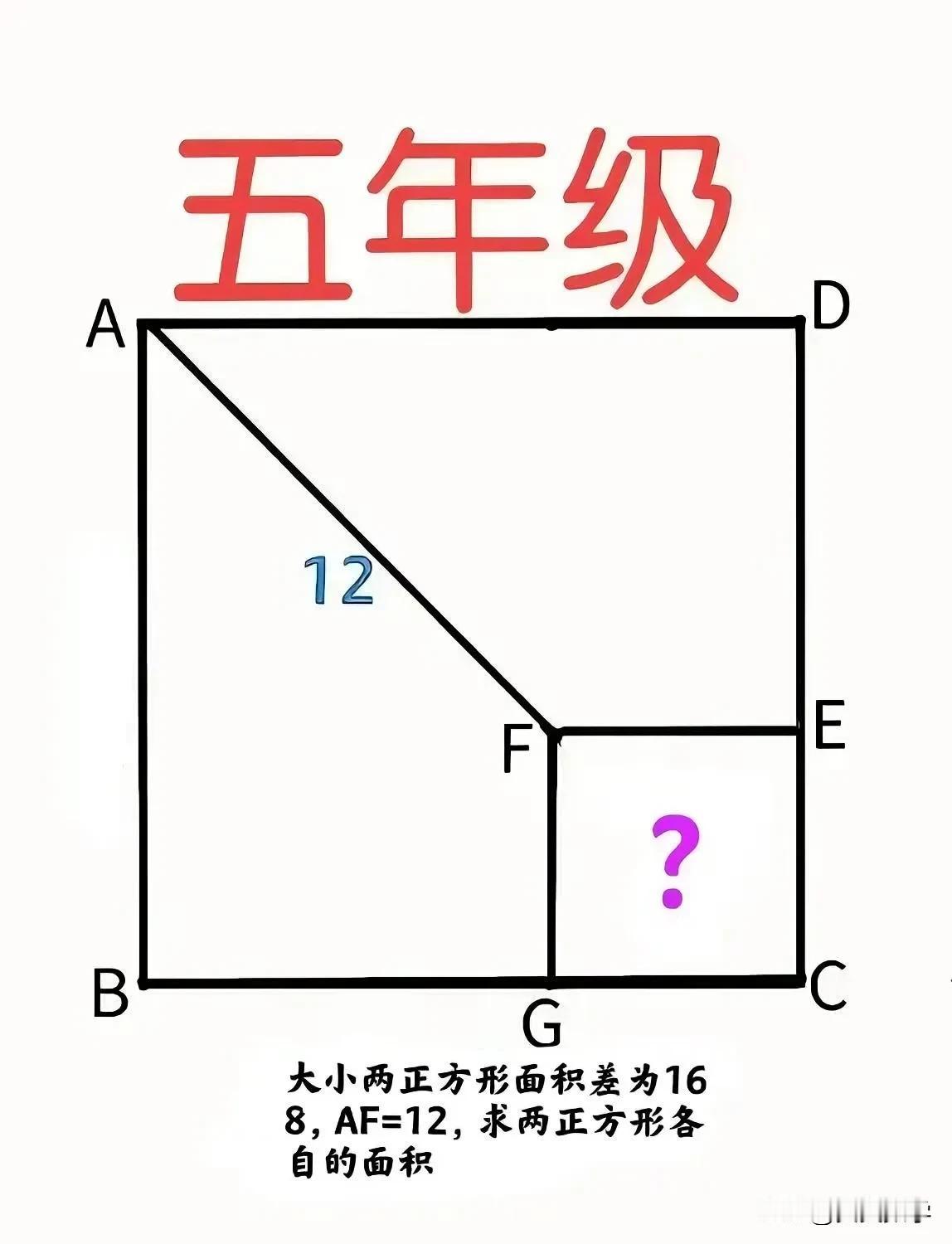
“全班都不会！”这是一道小学五年级数学竞赛题：正方形边长未知，咋求其面积？此题难在：仅用小学知识无法求出正方形边长，实际上其边长为无理数！ 如图，大正方形ABCD右下角有一小正方形CEFG，AF=12，两正方形面积差为168，求大小两个正方形的面积。 ——————————— 提示一：代数法，适合初中生！ ①大小正方形的边长分别记为a和b，则有a²-b²=168。 ②(a-b)²=72，由平方和及平方差公式可得3(a+b)=7(a-b)也即a=5b/2，从而b²=32。 提示二：分割法，适合五年级！ ①EF和GF分别与AB和AD相交于点M和N，则AMFN为正方形，BGFM和DEFN为两个一样的长方形。 ②S正AMFN=12×12÷2=72，故S长方形DEFN=S长方形BGFM=(168-72)÷2=48。 ③S正CEFG×S正AMFN=S长BGFM×S长DEFN，故S正CEFG=48×48÷72=32。 提示三：分割法，适合三年级！ 步骤①和②同于提示二。 ③'继续分割，以面积为8的小正方形为分割单元，则正方形AMFN、长方形BGFM和长方形DEFN分别可分成9、6和6个分割单元，从而正方形CEFG可分成4个面积为8的小正方形，也即其面积为32。