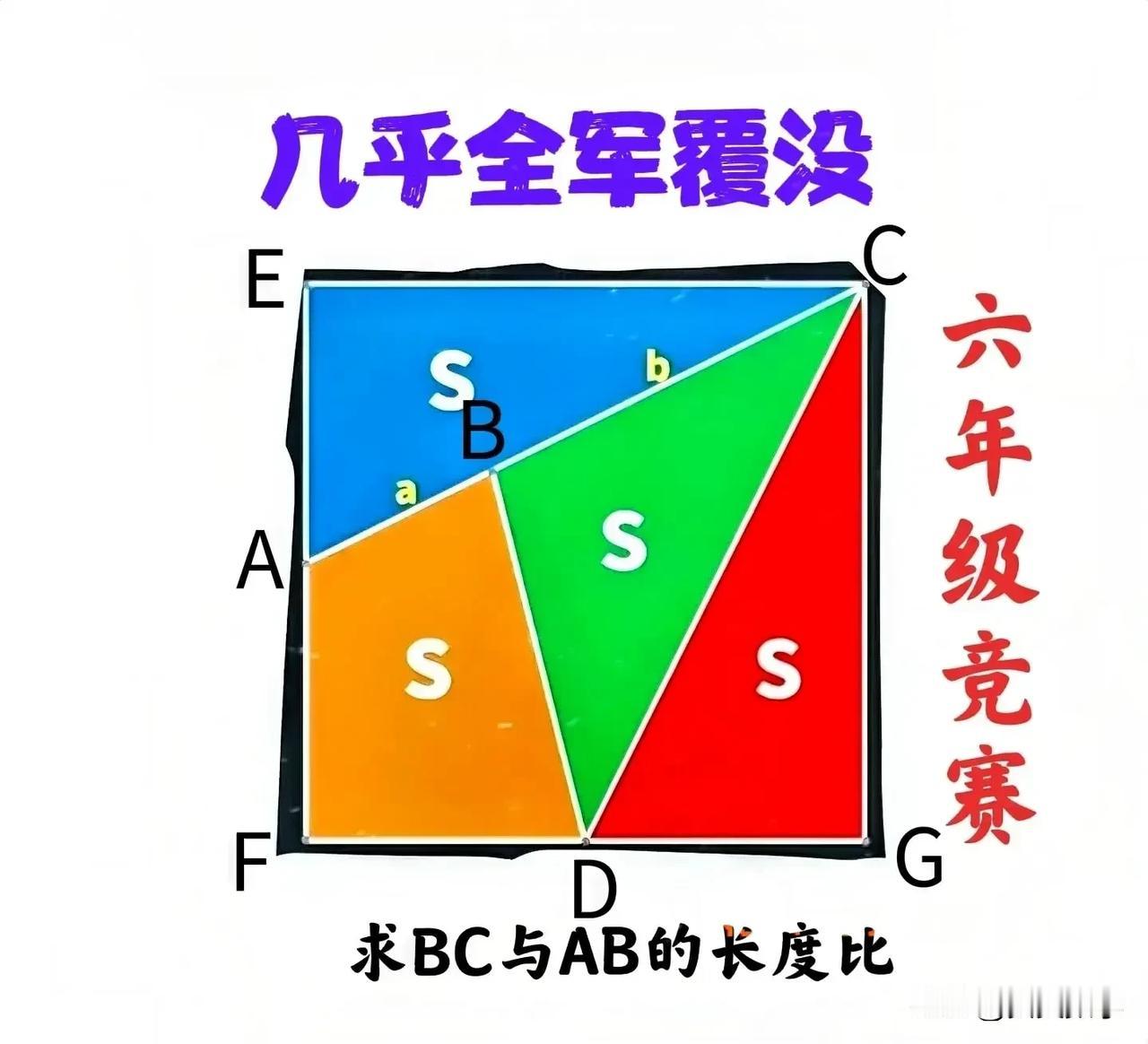
“几乎全军覆没！”只有极个别同学答对了，但冒然添加了条件“A、D为中点”，老师说“这是脱裤子放屁、多此一举！”这是一道小学五年级数学竞赛题： 如图，1个正方形被分割成面积相等的4个部分，求BC与AB的长度之比。 题眼或暗含条件：A、D均为正方形所在边上中点！ ——————————— 提示：等高三角形面积比等于底边之比！ ①找出暗含条件：由S△ACE=S△CDG=1/4S正方形CEFG即知，A、D分别为EF和FG上的中点。 ②连接AD，则S△ADF=1/8S正方形ABCD，从而S△ABD=1/8S正方形ABCD。 ③BC/AB=S△BCD/S△ABD=2。 友友们，怎么看？欢迎留言分享！ 小学数学 妙笔生花创作挑战