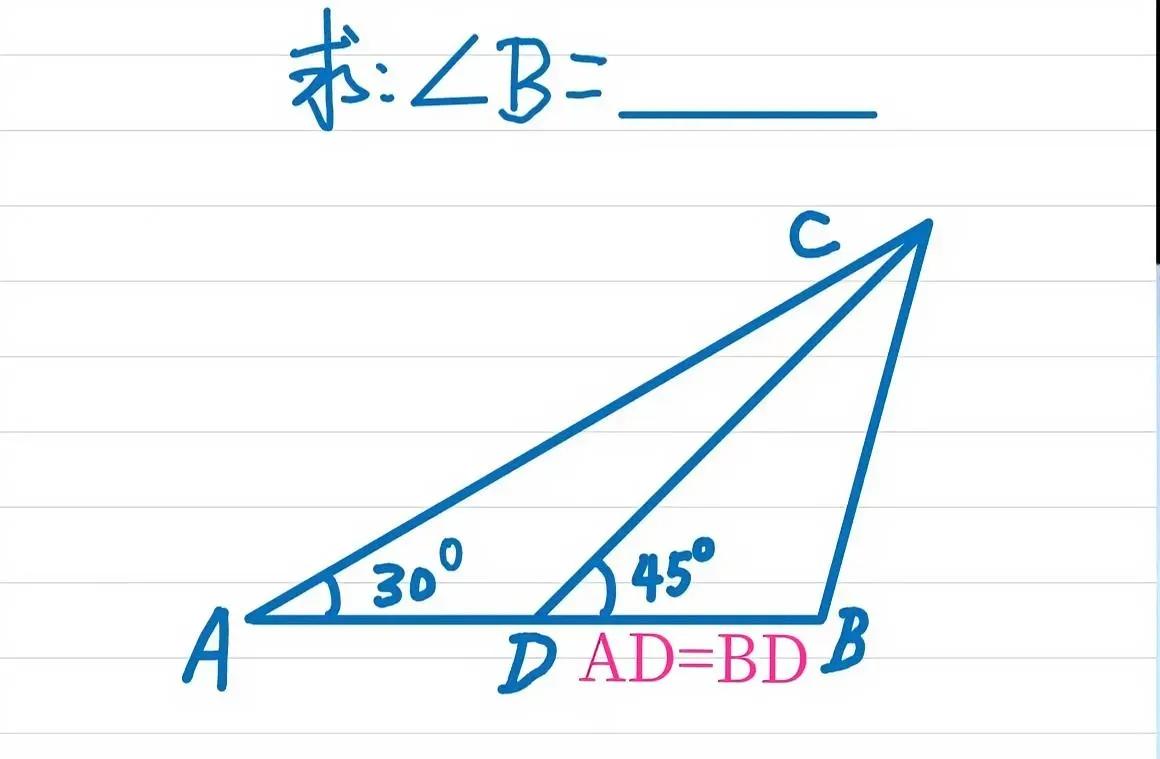
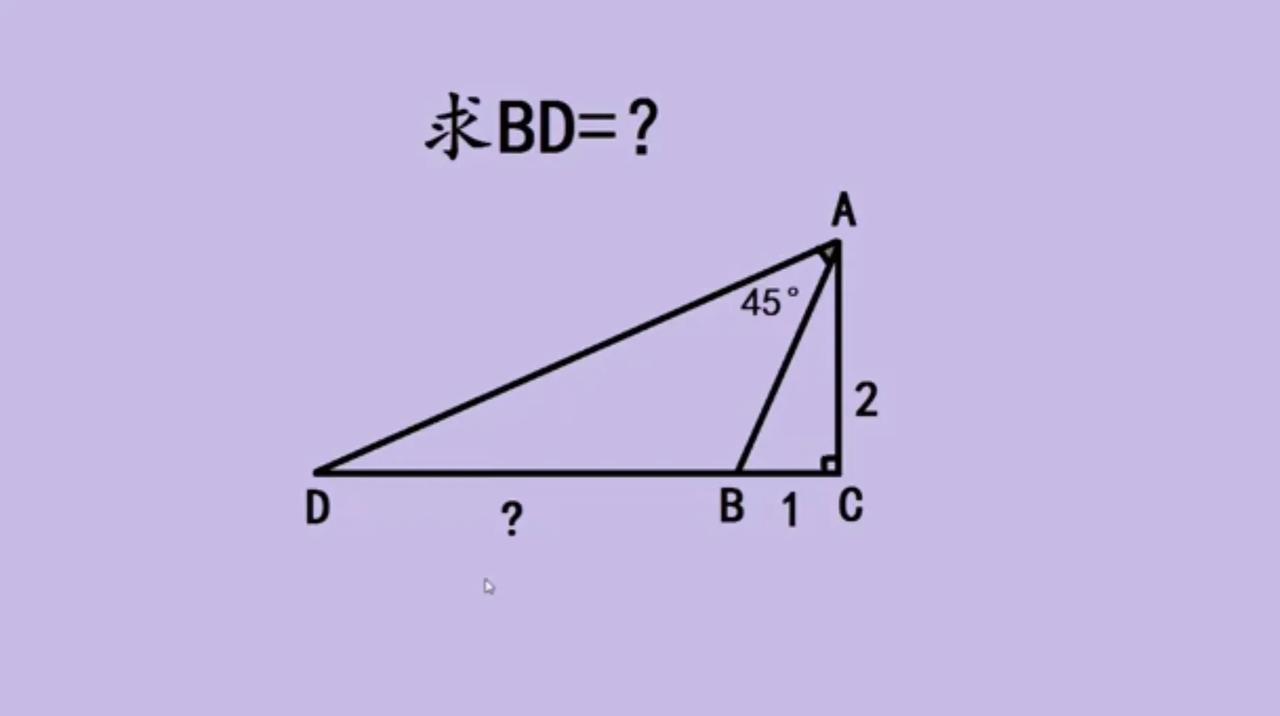
“利用三角形全等、求角度!”初中几何:如图,在三角形ABC中,D为AB的中点即AD=BD,∠A=30°,∠CDB=45°,求∠B=? ——————————— 提示一:以BD为边向上作等边三角形BDE! ①∠ACD=45°-30°=15°。 ②过点B作AC的垂线BE,则△BDE为等边三角形,从而∠ABE=60°,∠CDE=60°-45°=15°=∠ACD,故CE=DE。 ③∠AED=30°=∠A,故AD=DE=CE。 ④BE=BD=AD=CE,故△BCE为等腰三角形三角形,从而∠B=60°+45°=105° 提示二:图形翻折+等边三角形! ①将△ABC沿AC向左上翻折,翻折后的点B记为点E,连接BE与AC相交于点F,则BE垂直AC,且ABE与BDF均为等边三角形。 ②AD=BF=CF=BD=CF,故∠B=60°+45°=105°。 友友们,怎么看?欢迎留言分享! 发优质内容享分成